1. Задание № 52 

Сложность: III
Классификатор алгебры: 4\.2\. Неравенства первой и второй степени относительно показательных функций
Методы алгебры: Замена переменной
Показательные неравенства
i
Найдите сумму целых решений неравенства 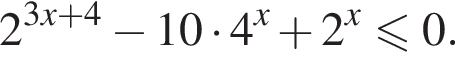
Решение. Решим неравенство:
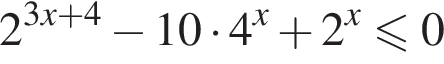
![]()
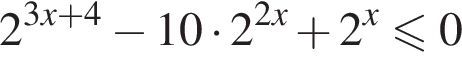
![]()
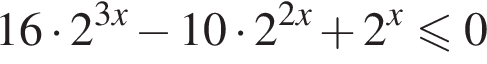
![]()
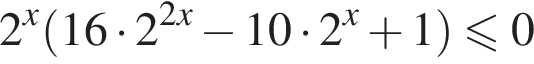
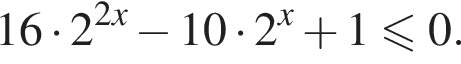
Сделаем замену ![]() тогда получим:
тогда получим:
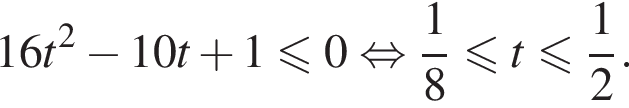
Вернемся к исходной переменной:
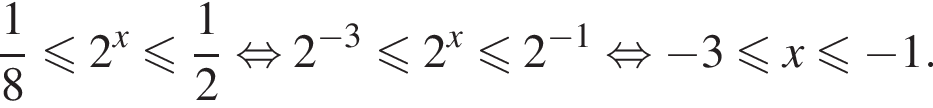
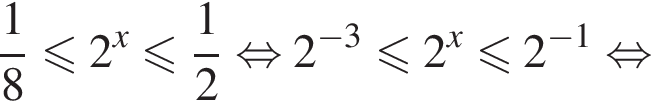

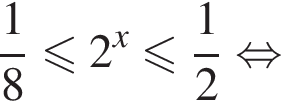
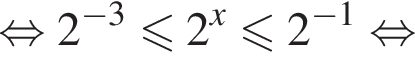

Следовательно, целыми решениями являются 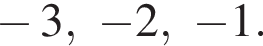 Их сумма равна −6.
Их сумма равна −6.
Ответ: −6.
Ответ: -6
52
-6
Сложность: III
Классификатор алгебры: 4\.2\. Неравенства первой и второй степени относительно показательных функций
Методы алгебры: Замена переменной
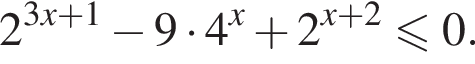
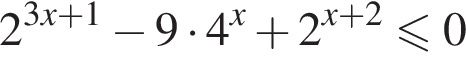
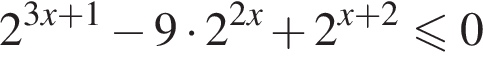
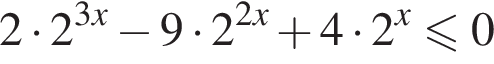
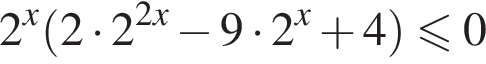
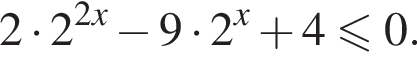
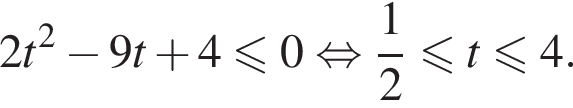
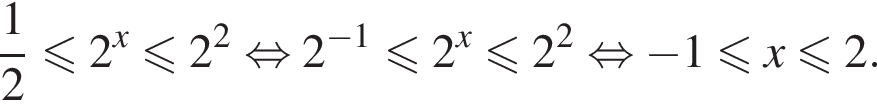
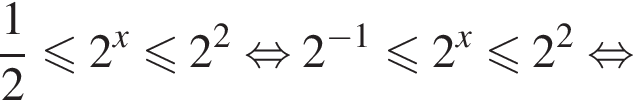

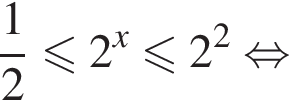
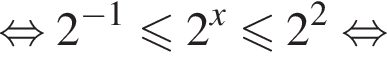
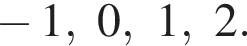 Их сумма равна 2.
Их сумма равна 2.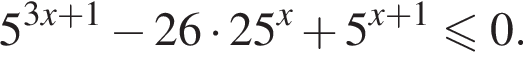
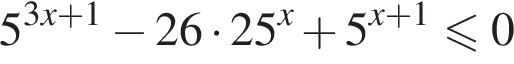
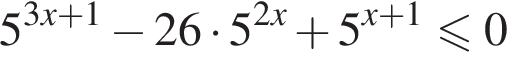
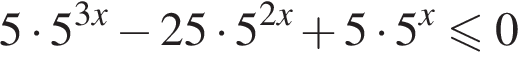
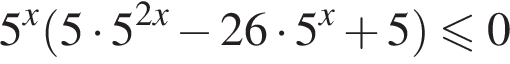
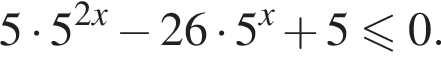
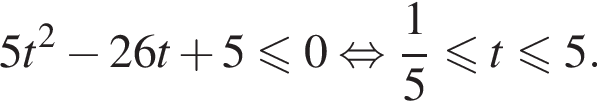
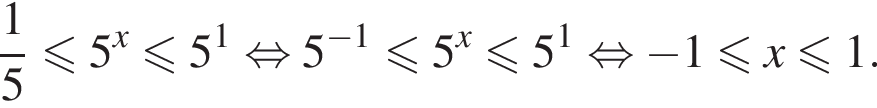
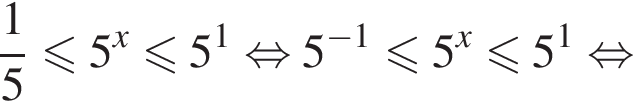

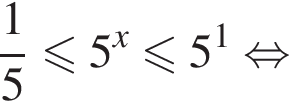
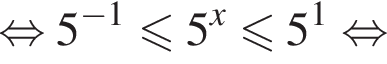
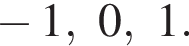 Их сумма равна 0.
Их сумма равна 0.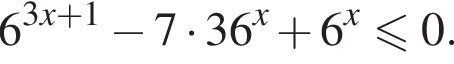
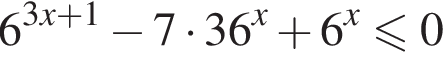
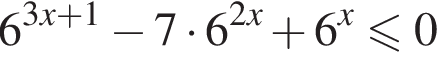
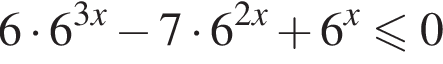
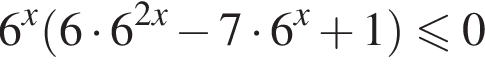
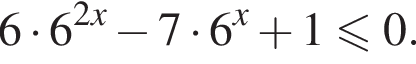
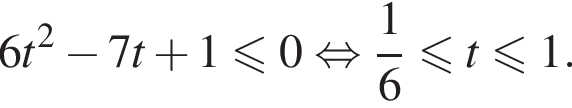
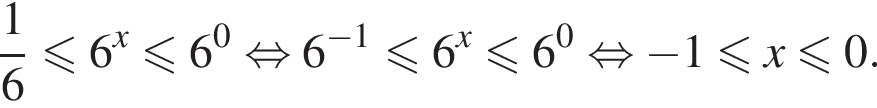
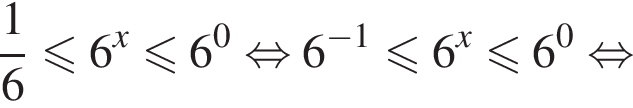

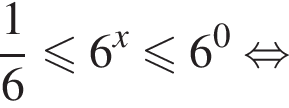
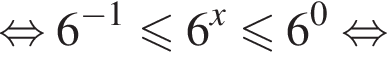
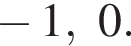 Их сумма равна −1.
Их сумма равна −1.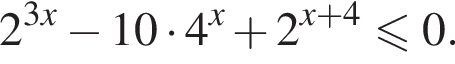
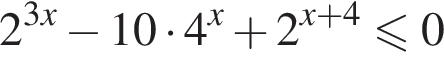
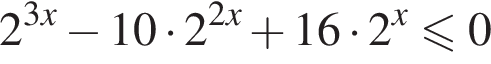
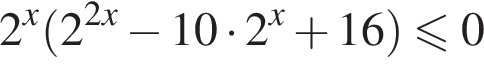
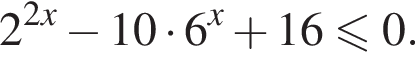
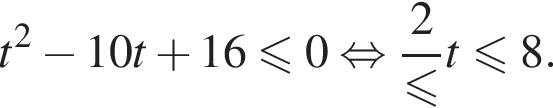
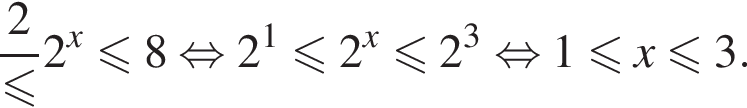
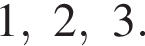 Их сумма равна 6.
Их сумма равна 6.